 |
EUROPAS NR.1 IN ROHRSYSTEMEN |
10.0 Vom Normalfall
abweichenden Bedingungen
10.0 Vom Normalfall |
10.1 Druckverlust im Rohr
Für den Normalfall wurde davon ausgegangen, daß Luft von 20° C bei einem Luftdruck von 1013 mbar, wie er auf Meereshöhe herrscht, in Rohren mit einer Oberflächenrauhigkeit von 0,15 mm gefördert wird. Die entsprechenden Verluste konnten der Tabelle 6.0 entnommen werden. Wenn andere Bedingungen vorliegen, muß der Druckverlust Dp errechnet werden: |
| Allgemeine Formel für
Druckabfall im geraden waagerechten Rohr mit konstantem Querschnitt: |
|
l (Lambda) = Rohrreibungszahl ohne Einheit |
l = Rohrlänge in m |
| d = lichter Rohrdurchmesser in m (bzw. hydraulischer Æ) | w = mittlere Geschwindigkeit im Rohr |
| r (Rho) = Dichte des Fördermediums in kg/m3 (siehe 10.3) | k = Oberflächenrauhigkeit in m (siehe 10.3) |
| u (Ypsilon ) = kinematische Viskosität des Fördermediums in m2/s (siehe 10.3) | |
| Bevor die Rohrreibungszahl l ermittelt werden kann, ist die Bestimmung der Reynolds-Zahl (Re) erforderlich, die als Verhältnis der Trägheitskraft zur Reibungskraft angesehen werden kann. |
|
Ermittlung der Rohrreibungszahl l
| Wenn Re kleiner ist als 2320 |
| Es liegt laminare Strömung vor, alle Partikel bewegen sich auf parallelen Bahnen zur Rohrachse. Die maximale Luftgeschwindigkeit in der Rohrachse ist bei Rohren mit Kreisquerschnitt doppelt so hoch wie die durchschnittliche Strömungsgeschwindigkeit (w). l ist unabhängig von der Wandrauhigkeit. Der Duckverlust ist proportional der Strömungsgeschwindigkeit. Für Rohre, die keinen Kreisquerschnitt aufweisen, ist bei laminarer Strömung eine Korrektur von l erforderlich. |
|
|
| Es herrscht turbulente Strömung; die Grenzschicht zwischen Rohrwand und Strömung deckt die Wandunebenheiten komplett ab - Rohr dadurch hydraulisch glatt. l nur abhängig von Re. Wegen des Geschwindigkeitsausgleichs durch die Turbulenzen ist die maximale Strömungsgeschwindigkeit in der Rohrmitte nur 13 bis 25 % höher als die durchschnittliche Geschwindigkeit (w). | 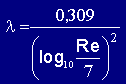 |
 |
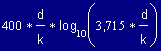 |
||
Wenn Re gößer als |
aber kleiner als | ||
| Turbulente Strömung;
Übergangsbereich Rauhigkeitsspitzen treten aus der Grenzschicht heraus. Häufigster Fall in lufttechnischen Anlagen. l von Re und d/k abhänging. |
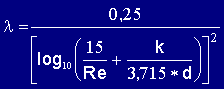 |
| l eingesetzt in
Druckverlustformel ergibt als Rechnereingabe: |
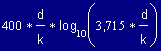 |
|
| Wenn Re gößer als | |
| Turbulente Strömung: die Wandunebenheiten sind größer als die Grenzschicht; Rohr dadurch hydraulisch rauh. l ist nur abhängig von der relativen Rauhigkeit d/k, aber nicht mehr von Re. |
|
10.3 Stoffwerte
| Kinematische Viskosität (n) und Dichte (r) von trockner Luft bei einem Druck von 1 bar absolutDie Viskosität von Luft bis zu 60% relativer Feuchtigkeit unterscheidet sich nur unwesentlich von trockener. 1 bar absolut entspricht in etwa dem Luftdruck 100 m über NN. J Temperatur in ° C; r Luftdichte in kg/m3 u kinematische Viskosität in mm2/s (da der Wert in mm2/s angegeben ist, muß er für die Verwendung in 10.0 wo er in m2/s benötigt wird, durch 1.000.000 geteilt werden.) |
|||||||||||
| J ° C | r kg/m3 | u mm2/s | J ° C | r kg/m3 | u mm2/s | J ° C | r kg/m3 | u mm2/s | J ° C | r kg/m3 | u mm2/s |
-180 |
3,851 |
1,720 |
-20 |
1,377 |
11,78 |
140 |
0,8425 |
28,07 |
450 |
0,4813 |
72,74 |
-160 |
3,126 |
2,558 |
0 |
1,275 |
13,52 |
160 |
0,8036 |
30,46 |
500 |
0,4502 |
81,35 |
-140 |
2,639 |
3,552 |
20 |
1,1881 |
15,35 |
180 |
0,7681 |
32,93 |
550 |
0,4228 |
90,31 |
-120 |
2,287 |
4,614 |
40 |
1,112 |
17,26 |
200 |
0,7356 |
35,47 |
600 |
0,3986 |
99,63 |
-100 |
2,019 |
5,829 |
60 |
1,045 |
19,27 |
250 |
0,6653 |
42,11 |
700 |
0,3576 |
119,3 |
-80 |
1,807 |
7,159 |
80 |
0,9859 |
21,35 |
300 |
0,6072 |
49,18 |
800 |
0,3243 |
140,2 |
-60 |
1,636 |
8,598 |
100 |
0,9329 |
23,51 |
350 |
0,5585 |
56,65 |
900 |
0,2967 |
162,4 |
-40 |
1,495 |
10,14 |
120 |
0,8854 |
25,75 |
400 |
0,5170 |
64,51 |
1000 |
0,2734 |
185,9 |
Beispiel: Umrechnung der Dichte (
r) für Luft 20 ° C bei 1,013 bar (nach Formel 10.5):
Kinematische Viskosität (u) und Dichte (r) verschiedener Gase bei 1bar (absolut) r
Luftdichte in kg/m3 |
|||||
Gas |
r |
u |
Gas |
r |
u |
Ammoniak NH3 ?° C |
0,7068 |
13,99 |
Wasserdampf H2O 100° C * |
0,5975 |
20,53 |
Kohlendioxid CO2 ~ 20° C |
1,815 |
8,106 |
Rauchgase 100° C |
0,95 |
20 |
Methan CH4 20° C |
0,67 |
15,6 |
Rauchgase 300° C |
0,63 |
45 |
Sauerstoff O2 20° C |
1,1 |
18 |
Erdgas 20° C |
0,78 |
12,8 |
Stickstoff N2 20° C |
1,15 |
15,3 |
Gichtgas 20° C |
1,2 |
14 |
Wasserstoff H2 0° C |
0,087 |
97 |
Stadtgas 20° C |
0,5 |
26 |
| * gesättigt bei 1013 mbar |
Luftdruck in verschiedenen Höhenlagen - von NN (Meereshöhe) gemessen |
|||||||||||
Höhe |
Druck |
Höhe |
Druck |
Höhe |
Druck |
Höhe |
Druck |
Höhe |
Druck |
Höhe |
Druck |
-700 |
0 |
1,01325 |
350 |
0,97192 |
700 |
0,93192 |
1100 |
0,88792 |
1800 |
0,81459 |
|
-600 |
50 |
1,00725 |
400 |
0,96592 |
750 |
0,92659 |
1200 |
0,87726 |
1900 |
0,80460 |
|
-500 |
100 |
1,00125 |
450 |
0,96058 |
800 |
0,92059 |
1300 |
0,86659 |
2000 |
0,79460 |
|
-400 |
150 |
0,99525 |
500 |
0,95458 |
850 |
0,91525 |
1400 |
0,85592 |
2500 |
0,74660 |
|
-300 |
200 |
0,98925 |
550 |
0,94792 |
900 |
0,90992 |
1500 |
0,84526 |
3000 |
0,70127 |
|
-200 |
250 |
0,98325 |
600 |
0,94258 |
950 |
0,90392 |
1600 |
0,83526 |
3500 |
0,65794 |
|
-100 |
300 |
0,97791 |
650 |
0,93725 |
1000 |
0,89859 |
1700 |
0,82459 |
4000 |
0,61661 |
|
Rohrrauhigkeit
(k) |
|||
Rohrart |
k (mm) |
Rohrart |
k (mm) |
gezogenes Rohr aus Kupfer ;
Messing; |
0,0013 |
nahtlose Stahlrohre gezogen |
0,02.......0,1 |
nahtlose Stahlrohre gebeizt |
0,03....0,04 |
||
PVC-hart und |
0,0015 |
längsgeschweißte Stahlrohre Walzhaut |
0,04......0,1 |
Stahlrohre feuerverzinkt |
0,1......0,16 |
||
Rohre aus Gusseisen |
0,25....0,5 |
Stahlrohre gleichm. Rostnarben |
0,15......0,4 |
Asbest- Zementrohre |
0,1......0,6 |
Stahlrohre leichte Verkrustungen |
1........1,5 |
Holzverkleidung ungehobelt |
0,7......2,5 |
Stahlrohre starke Verkrustungen |
2..........4 |
Betonrohre rauh |
1,2......3,0 |
Wickelfalzrohr |
0,1.. ....2,0 |
Betonrohre mit Glattstrich |
0,3.... 0,8 |
Blechkanäle gefalzt, 1 Verbindung pro m |
0,15......0,2 |
Backsteinmauerwerk gefugt |
1,3 |
flexible Rohre und Schläuche |
0,2......3,0 |
gemauerte Kanäle roher Bruchstein |
8........15 |
||
Für Rohrstrecken mit Stoßkanten oder Vertiefungen an den Verbindungen k- Wert erhöhen |
|||
10.4 Umrechnung der Stoffwerte
| Verwendete Formelzeichen: |
|
| pabs n | Absoluter Druck des Gases im Normzustand (oder eines bekannten Zustands) in Pa bzw. bar |
| pabs x | Absoluter Druck des Gases im gesuchten Zustand in Pa bzw. bar |
| Tn | Temperatur in ° K des Gases im Normzustand (oder eines bekannten Zustands) |
| Tx | Temperatur in ° K des Gases im gesuchten Zustand |
| Temperatur in Kelvingraden (° K) = Temperatur in ° C + 273,15 (20° C = 293,15° K) | |
| Voln | Volumen des Gases im Normzustand (oder eines bekannten Zustands) in m3 |
| Volx | Volumen des Gases im gesuchten Zustand in m3 |
| rn | Dichte des Gases im Normzustand (oder eines bekannten Zustands) in kg/m3 |
| rx | Dichte des Gases im gesuchten Zustand in kg/m3 |
| Allgemeine Zustandsgleichung idealer Gase: |
|
Umrechnung der Gasdichte (r) |
|
Gasdichte (r) |
|
Werte für die Dichte (r) von trockner Luft: |
|
Umrechnung der kinematischen
Viskosität (u) |
|
| Die dynamische Viskosität (h) nimmt mit der Temperatur zu, ist jedoch im
Bereich von 0,1 bis 10 bar weitgehend unabhängig vom Druck, daher wird sie bevorzugt
genannt. Die dynamische Viskosität wird auch in Pa * s angegeben, dieser Wert ist identisch mit kg/(m*s) |
|
10.8 Allgemeine Druckverlustberechnung
Die Berechnung kann wie im Beispiel 2.0
erfolgen, jedoch ist der Verlust pro Meter Rohr nach den Formeln 10.0 zu ermitteln. Bei größeren Druck- und
Temperaturunterschieden im Leitungsverlauf ist die Änderung der Gasdichte zu beachten. Um nicht bei jeder einzelnen vom Normalfall
abweichenden Bedingung eine andere Berechnungsweise durchzuführen, könnte nach unten
angegebenem Schema verfahren werden, in dem alle gängigen Fälle abgedeckt sind. Um Umrechnungen zu vermeiden, wird beim Volumenstrom als Einheit Meter pro Sekunde verwendet. Außerdem werden die Drücke nicht mehr als Unter- bzw. Überdrücke relativ zur Atmosphäre sondern als Absolutdrücke angegeben. |
Vorgehensweise:
Die Druckverluste der Teilstrecken können nicht mehr unabhängig voneinander ermittelt und anschließend zum Gesamtdruckverlust der Anlage addiert werden, da die Luftdichte und damit auch die Luftgeschwindigkeit und der Volumenstrom von dem Druck in der Teilstrecke abhängen, der wiederum von den Druckverlusten in den vorherigen Teilstrecken mit bestimmt wird. Vom Umgebungsdruck (Atmosphärendruck) im Bereich des Saugstutzens ausgehend wird über den Druckverlust der Teilstrecke der absolute Druck am Ende der 1. Teilstrecke ermittelt. Dieser Druck ist der Anfangsdruck für die nächste Teilstrecke. Der Enddruck in der letzten saugseitigen Teilstrecke ist dann der Druck im Ventilatorsaugstutzen. (Siehe auch 1.9) Auf der Druckseite des Ventilators wird analog vom Ausblasstutzen der Rohrleitung aus verfahren. Sollten größere Höhenunterschiede zwischen den verschiedenen Ansaug- bzw. Ausblasstutzen bestehen und außerdem das Fördergas einen andere Dichte als die Umgebungsluft aufweisen, sind auch die unterschiedlichen Atmosphärendrücke im Bereich der Stutzen zu beachten. Zur Begriffsbestimmung von Anfang und Ende der Teilstrecken wird die Flussrichtung des Gasstroms angesehen, d.h. am Ende der Ausblasleitung herrscht Atmosphärendruck, während am Anfang dieser Teilstrecke der Druck um den Druckverlust der Teilstrecke höher sein muss. Da in dem jeweiligem Druck der Teilstrecke die bis dahin angefallenen Druckverluste aufsummiert enthalten sind, wird gleichzeitig der Hauptstrang ermittelt. Die Nebenstränge müssen bei der Einmündung in den Hauptstrang den gleichen Druck aufweisen, wie er im Hauptstrang an dieser Stelle herrscht. Die Differenz ist als zusätzlicher Drosselverlust anzusetzen, andernfalls würde in dem Nebenstrang mehr Gas gefördert als berechnet. Der zum Schluss ermittelte Anfangsdruck der
1. ausblasseitigen Teilstrecke ist auch der Druck im Ventilatorausblasstutzen. Die
Differenz zwischen Saug- und Druckstutzen des Ventilators ist der Gesamtdruckverlust der
Anlage (DpgeA)
und muss vom Ventilator als totale Druckdifferenz (Dpt) aufgebracht werden. Um die Genauigkeit der Berechnung zu erhöhen, können Teilstrecken mit hohen Druckverlusten oder großen Temperaturänderungen in mehrere Teilstrecken unterteilt werden, die bei der Berechnung dann unterschiedliche Gasdichten und damit auch andere Geschwindigkeiten aufweisen. |
Zur besseren Übersicht der Druckverlustberechnung wurde unten je ein Formblatt für saugseitige und druckseitige Teilstrecken erstellt. Ob zuerst die saugseitigen oder druckseitigen Teilstrecken berechnet werden spielt keine Rolle. Bedingung ist jedoch, daß bei den saugseitigen am Anfang der Leitung mit dem Ansaugstutzen begonnen wird und bei den druckseitigen mit dem Ende der Leitung, dem Ausblasstutzen. zu Zeile [1] Damit der Druckverlust einer Teilstrecke (TS) ermittelt werden kann muss die mittlere Dichte des Gases in der TS bekannt sein. Diese hängt jedoch von dem mittlerem Druck in der Teilstrecke ab, der sich aber erst bestimmen lässt, wenn die Druckverluste bekannt sind. Daher ist der Druck für die Zeile [11] erst einmal überschlägig zu ermitteln, z.B. nach Tabelle 6.0 und in Zeile [1] einzutragen. zu Zeile [2] Hier wird der mittlere
Druck (pM) der TS festgelegt. Nachdem der mittlere Druck (pM) in etwa festgelegt wurde, können Gasdichte, Volumenstrom, Gasgeschwindigkeit und dynamischer Druck in der Teilstrecke errechnet werden. zu Zeile 3 Druckverlust durch Einzelwiderstände (Summe z * pdyM) siehe auch 2.3 und 8.0
|
| zu Zeile 5 Differenzdruck durch Schwerkraftdruck ("hydrostatischer Druck") | ||
Sollten die Teilstrecken
Höhenunterschiede aufweisen, ist der daraus resultierende "hydrostatische"
Druck zu berücksichtigen. |
h = Höhe der Gassäule in m |
 |
Um die Druckdifferenzen durch den hydrostatischen Druck (Dphydro) korrekt zuordnen zu können, ist die Höhendifferenz der Teilstrecke zwischen Anfangs- und Endpunkt (Dh) bei in Flussrichtung steigenden Leitungen positiv einzusetzen und bei in Flussrichtung fallenden Leitungen negativ. |
|
zu Zeile 9 bis 11 Bei
verzweigten Rohrsystemen brauchen erkennbare Nebenstränge nicht berechnet werden, da sie
für die vom Ventilator zur erzeugende Druckdifferenz nicht relevant sind. Ist nicht erkennbar, ob die Teilstrecke zum
Hauptstrang (Weg mit den größten Druckdifferenzen) gehört, oder einen Nebenstrang
bildet, ist nach Berechnung der Zeile [9] zu unterbrechen und erst der andere Weg bis zu
dem Punkt, wo sich die beiden Stränge treffen, zu berechnen. Sollte sich, nachdem Zeile [11] ermittelt ist, herausstellen, dass größere Abweichungen zu dem angenommenen Druck in Zeile [1] besteht, ist die Berechnung der Teilstrecke mit dem jetzt ermitteltem Wert zu wiederholen. |