Druckverlustberechnung: Vom Normalfall abweichende Bedingungen 10.9

EUROPAS NR.1 IN ROHRSYSTEMEN

Vom Normalfall
abweichenden Bedingungen

10.9 Beispiel Druckverlustberechnung

Fördermedium Luft.
Normalzustand: Temperatur 20° C, Dichte (r) = 1,2 kg/m³, kinematische Viskosität (u) = 15,15 mm²/s. Volumenstromangaben und Luftgeschwindigkeiten in der Zeichnung auf Gaszustand bei Atmosphärendruck in 0 m Höhe (Normalzustand) bezogen.
Rohrrauhigkeit (k) 0,15 mm. Gleichbleibende Temperatur von 20° C im Leitungsverlauf angenommen

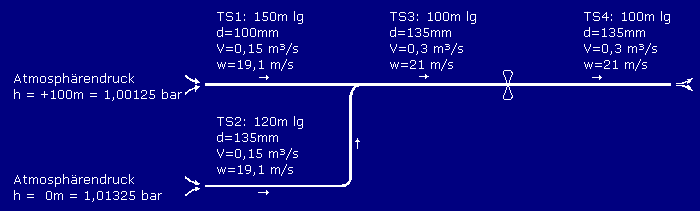
b10_9.gif (3363 Byte)

*Druckverlustberechnung Rohrleitungen saugseitig* des Ventilators.** Mit der vom Ventilator entferntesten Teilstrecke beginnen. Druckangaben als Absolutdrücke in Pa								TS Nr. 1
Rohrdurchmesser lichte Weite (d) in Meter						0,1	Gas- zu- stand auf den Normal- zustand bezogen Indize (n)	Gas auf mittlere Zustands- werte in der Teil- strecke bezogen Indize (M)
Rohrlänge (l) in m						150
Rohrrauhigkeit (k) ® nach 10.3 (mm * 10^-3 = m) in Meter						0,00015
Höhendifferenz zwischen Anfangs- und Endpunkt der TS (Dh) in m Vorzeichen: in Flussrichtung steigend Dh+ in Flussricht. fallend Dh -						0
Grad K = Grad C + 273				Temperatur des Fördergases (T) in Grad K			293	293
r_M = r_nT_n p_M / (T_M*p_n) in kg/m³				Gasdichte (r) in kg / m³			1,2	1,126
V_M = V_n * r_n / r_M in m³/s				Volumenstrom (V) in m³/Sekunde			0,15	0,16
w_M = V_M / (d² * p/4) in m/s				Gasgeschwindigkeit (w) in m/s			19,1	20,4
Formel nur bei Temperaturgleichheit: u_M = u_n * p_n / p_M in m²/s				kinematische Viskosität (u) in m²/s (mm²/s * 10^-6 = m²/s)			15,15 *10^-6	16,14 *10^-6
p_{dyM =} r_M * w_M² / 2 in Pa				mittlerer dynamischer Druck der Teilstrecke (p_dyM) in Pa				233
Einzelwiderstände:				(Bezeichnung für nachfolgend, vorher, Anfang bzw. Ende bei den Teilstrecken immer in Flussrichtung gesehen.)
Bezeichnung	Stck	z	Stck*z
Ansaugstutzen	1	0,9	0,9	Druck (p_n) entsprechend dem für den Normalzustand des Gases definierten Wert in Pa				101 300
				Geschätzter Druck am Ende der Teilstrecke in Pa. Bei großen Abweichungen, von dem sich später in Zeile 11 ergebenem Wert, ist die Rech- nung mit dem neuen Wert zu wiederholen. Wenn Nebenstrang: Wert aus Zeile 11 übernehmen				[1] 90 000

Abzweig gerader Durchgang	1	0,1	0,1	Mittlerer statischer Druck (p_M) in der TS in Pa (Zeile 1 + Zeile 8) / 2 - p_dyM				[2] 95 062

Einzelwiderstände Summe ( Stck*z )			1,0	Þ * p_dyM= 233	233 Pa		[3] Druckverlust durch Einzelwiderstände
Nach Formeln 10.1 Überwiegend im Übergangsbereich nach 10.2: Dp = { 0,25 / [ ( log₁₀ (15 * u_M / (w_M * d) + k / (3,715 * d) ))² ] } * l * r_M * w_M² / (d * 2) in Pa					8 120 Pa		[4] Druckverlust durch Rohrreibung
p_hydro = Dh * r_M * 9,81 m/s² Vorzeichen beachten (negativer Wert von Dh ergibt Druckgewinn)					0 Pa		[5] Druckverlust durch hydrostatischen Druck
Nach Herstellerangaben					0 Pa		[6] Druckverlust durch Geräte
Summe der Zeilen 3 bis 6					8 353 Pa		[7] Druckverlust der Teilstrecke

Entsprechend dem Enddruck der vorherigen TS, bzw. am Anfang der Leitungen Atmosphärendruck im Bereich des Ansaugstutzens in Pa (1,013 bar = 101 300 Pa)					100 125 Pa		[8] Druck am Anfang der Teilstrecke
Zeile 8 minus Zeile 7 Nur für verzweigenden Leitungen: Wenn dieser Druck höher ist als der Druck an der Stelle, wo diese TS in den anderen Strang mündet, ist diese TS ein Nebenstrang und zu drosseln. Wenn dieser Druck niedriger ist als der Druck im Strang, wo er einmündet, gehört diese TS zum Hauptstrang, und der andere Strang ist entsprechend zu drosseln.					91 771 Pa		[9] Druck am Ende der Teilstrecke (ohne Drosselung)
Zeile 11 minus Zeile 9 Für Nebenstrang: Drosselung zur Verminderung des Enddrucks der Teilstrecke.					0 Pa		[10] zusätzlicher Drosselverlust
Wenn Hauptstrang : Wert aus Zeile 9 übernehmen. Wenn Nebenstrang: Druck des Hauptstranges im Bereich der Einmündung hier übernehmen. Der Wert ist gleichzeitig der Anfangsdruck für anschließende TS					91 771 Pa		[11] Druck am Ende der Teilstrecke (Um die Druckverluste niedriger als der Anfangsdruck)

*Druckverlustberechnung Rohrleitungen saugseitig* des Ventilators.** Mit der vom Ventilator entferntesten Teilstrecke beginnen. Druckangaben als Absolutdrücke in Pa								TS Nr. 2
Rohrdurchmesser lichte Weite (d) in Meter						0,1	Gas- zu- stand auf den Normal- zustand bezogen Indize (n)	Gas auf mittlere Zustands- werte in der Teil- strecke bezogen Indize (M)
Rohrlänge (l) in m						120
Rohrrauhigkeit (k) ® nach 10.3 (mm * 10^-3 = m) in Meter						0,00015
Höhendifferenz zwischen Anfangs- und Endpunkt der TS (Dh) in m Vorzeichen: in Flussrichtung steigend Dh+ in Flussricht. fallend Dh -						+100
Grad K = Grad C + 273				Temperatur des Fördergases (T) in Grad K			293	293
r_M = r_nT_n p_M / (T_M*p_n) in kg/m³				Gasdichte (r) in kg / m³			1,2	1,13
V_M = V_n * r_n / r_M in m³/s				Volumenstrom (V) in m³/Sekunde			0,15	0,16
w_M = V_M / (d² * p/4) in m/s				Gasgeschwindigkeit (w) in m/s			19,1	20,2
Formel nur bei Temperaturgleichheit: u_M = u_n * p_n / p_M in m²/s				kinematische Viskosität (u) in m²/s (mm²/s * 10^-6 = m²/s)			15,15 *10^-6	16,00 *10^-6
p_{dyM =} r_M * w_M² / 2 in Pa				mittlerer dynamischer Druck der Teilstrecke (p_dyM) in Pa				232
Einzelwiderstände:				(Bezeichnung für nachfolgend, vorher, Anfang bzw. Ende bei den Teilstrecken immer in Flussrichtung gesehen.)
Bezeichnung	Stck	z	Stck*z
Ansaugstutzen	1	0,6	0,6	Druck (p_n) entsprechend dem für den Normalzustand des Gases definierten Wert in Pa				101 300
Bogen 90°	1	0,2	0,2	Geschätzter Druck am Ende der Teilstrecke in Pa. Bei großen Abweichungen, von dem sich später in Zeile 11 ergebenem Wert, ist die Rech- nung mit dem neuen Wert zu wiederholen. Wenn Nebenstrang: Wert aus Zeile 11 übernehmen				[1] 90 000
Bogen 60°	1	0,2	0,2
Abzweig -Abgang	1	0,2	0,2	Mittlerer statischer Druck (p_M) in der TS in Pa (Zeile 1 + Zeile 8) / 2 - p_dyM				[2] 95 662

Einzelwiderstände: Summe ( Stck*z )			1,2	Þ * p_dyM= 232	278 Pa		[3] Druckverlust durch Einzelwiderstände
Nach Formeln 10.1 Überwiegend im Übergangsbereich nach 10.2: Dp = { 0,25 / [ ( log₁₀ (15 * u_M / (w_M * d) + k / (3,715 * d) ))² ] } * l * r_M * w_M² / (d * 2) in Pa					6 456 Pa		[4] Druckverlust durch Rohrreibung
p_hydro = Dh * r_M * 9,81 m/s² Vorzeichen beachten (negativer Wert von Dh ergibt Druckgewinn)					1 112 Pa		[5] Druckverlust durch hydrostatischen Druck
Nach Herstellerangaben					0 Pa		[6] Druckverlust durch Geräte
Summe der Zeilen 3 bis 6					7 846 Pa		[7] Druckverlust der Teilstrecke

Entsprechend dem Enddruck der vorherigen TS, bzw. am Anfang der Leitungen Atmosphärendruck im Bereich des Ansaugstutzens in Pa (1,013 bar = 101 300 Pa)					101 325 Pa		[8] Druck am Anfang der Teilstrecke
Zeile 8 minus Zeile 7 Nur für verzweigenden Leitungen: Wenn dieser Druck höher ist als der Druck an der Stelle, wo diese TS in den anderen Strang mündet, ist diese TS ein Nebenstrang und zu drosseln. Wenn dieser Druck niedriger ist als der Druck im Strang, wo er einmündet, gehört diese TS zum Hauptstrang, und der andere Strang ist entsprechend zu drosseln.					93 479 Pa		[9] Druck am Ende der Teilstrecke (ohne Drosselung)
Zeile 11 minus Zeile 9 Für Nebenstrang: Drosselung zur Verminderung des Enddrucks der Teilstrecke.					1 708 Pa		[10] zusätzlicher Drosselverlust
Wenn Hauptstrang : Wert aus Zeile 9 übernehmen. Wenn Nebenstrang: Druck des Hauptstranges im Bereich der Einmündung hier übernehmen. Der Wert ist gleichzeitig der Anfangsdruck für anschließende TS					91 771 Pa		[11] Druck am Ende der Teilstrecke (Um die Druckverluste niedriger als der Anfangsdruck)

*Druckverlustberechnung Rohrleitungen saugseitig* des Ventilators.** Mit der vom Ventilator entferntesten Teilstrecke beginnen. Druckangaben als Absolutdrücke in Pa								TS Nr. 3
Rohrdurchmesser lichte Weite (d) in Meter						0,135	Gas- zu- stand auf den Normal- zustand bezogen Indize (n)	Gas auf mittlere Zustands- werte in der Teil- strecke bezogen Indize (M)
Rohrlänge (l) in m						100
Rohrrauhigkeit (k) ® nach 10.3 (mm * 10^-3 = m) in Meter						0,00015
Höhendifferenz zwischen Anfangs- und Endpunkt der TS (Dh) in m Vorzeichen: in Flussrichtung steigend Dh+ in Flussricht. fallend Dh -						0
Grad K = Grad C + 273				Temperatur des Fördergases (T) in Grad K			293	293
r_M = r_nT_n p_M / (T_M*p_n) in kg/m³				Gasdichte (r) in kg / m³			1,2	1,059
V_M = V_n * r_n / r_M in m³/s				Volumenstrom (V) in m³/Sekunde			0,3	0,34
w_M = V_M / (d² * p/4) in m/s				Gasgeschwindigkeit (w) in m/s			21	23,8
Formel nur bei Temperaturgleichheit: u_M = u_n * p_n / p_M in m²/s				kinematische Viskosität (u) in m²/s (mm²/s * 10^-6 = m²/s)			15,15 *10^-6	17,17 *10^-6
p_{dyM =} r_M * w_M² / 2 in Pa				mittlerer dynamischer Druck der Teilstrecke (p_dyM) in Pa				299
Einzelwiderstände:				(Bezeichnung für nachfolgend, vorher, Anfang bzw. Ende bei den Teilstrecken immer in Flussrichtung gesehen.)
Bezeichnung	Stck	z	Stck*z
Ansaugstutzen				Druck (p_n) entsprechend dem für den Normalzustand des Gases definierten Wert in Pa				101 300
Bogen 90°				Geschätzter Druck am Ende der Teilstrecke in Pa. Bei großen Abweichungen, von dem sich später in Zeile 11 ergebenem Wert, ist die Rech- nung mit dem neuen Wert zu wiederholen. Wenn Nebenstrang: Wert aus Zeile 11 übernehmen				[1] 87 000
Bogen 60°
Abzweig				Mittlerer statischer Druck (p_M) in der TS in Pa (Zeile 1 + Zeile 8) / 2 - p_dyM				[2] 89 385

Einzelwiderstände: Summe ( Stck*z )			0	Þ * p_dyM= 0	0 Pa		[3] Druckverlust durch Einzelwiderstände
Nach Formeln 10.1 Überwiegend im Übergangsbereich nach 10.2: Dp = { 0,25 / [ ( log₁₀ (15 * u_M / (w_M * d) + k / (3,715 * d) ))² ] } * l * r_M * w_M² / (d * 2) in Pa					4 727 Pa		[4] Druckverlust durch Rohrreibung
p_hydro = Dh * r_M * 9,81 m/s² Vorzeichen beachten (negativer Wert von Dh ergibt Druckgewinn)					0 Pa		[5] Druckverlust durch hydrostatischen Druck
Nach Herstellerangaben					0 Pa		[6] Druckverlust durch Geräte
Summe der Zeilen 3 bis 6					4 727 Pa		[7] Druckverlust der Teilstrecke

Entsprechend dem Enddruck der vorherigen TS, bzw. am Anfang der Leitungen Atmosphärendruck im Bereich des Ansaugstutzens in Pa (1,013 bar = 101 300 Pa)					91 771 Pa		[8] Druck am Anfang der Teilstrecke
Zeile 8 minus Zeile 7 Nur für verzweigenden Leitungen: Wenn dieser Druck höher ist als der Druck an der Stelle, wo diese TS in den anderen Strang mündet, ist diese TS ein Nebenstrang und zu drosseln. Wenn dieser Druck niedriger ist als der Druck im Strang, wo er einmündet, gehört diese TS zum Hauptstrang, und der andere Strang ist entsprechend zu drosseln.					87 044 Pa		[9] Druck am Ende der Teilstrecke (ohne Drosselung)
Zeile 11 minus Zeile 9 Für Nebenstrang: Drosselung zur Verminderung des Enddrucks der Teilstrecke.					0 Pa		[10] zusätzlicher Drosselverlust
Wenn Hauptstrang : Wert aus Zeile 9 übernehmen. Wenn Nebenstrang: Druck des Hauptstranges im Bereich der Einmündung hier übernehmen. Der Wert ist gleichzeitig der Anfangsdruck für anschließende TS					87 044 Pa		[11] Druck am Ende der Teilstrecke (Um die Druckverluste niedriger als der Anfangsdruck)

*Druckverlustberechnung Rohrleitungen druckseitig* des Ventilators.** Mit der vom Ventilator entferntesten Teilstrecke beginnen. Druckangaben als Absolutdrücke in Pa								TS Nr. 4
Rohrdurchmesser lichte Weite (d) in Meter						0,135	Gas- zu- stand auf den Normal- zustand bezogen Indize (n)	Gas auf mittlere Zustands- werte in der Teil- strecke bezogen Indize (M)
Rohrlänge (l) in m						100
Rohrrauhigkeit (k) ® nach 10.3 (mm * 10^-3 = m) in Meter						0,00015
Höhendifferenz zwischen Anfangs- und Endpunkt der TS (Dh) in m Vorzeichen: in Flussrichtung steigend Dh+ in Flussricht. fallend Dh -						0
Grad K = Grad C + 273				Temperatur des Fördergases (T) in Grad K			293	293
r_M = r_nT_n p_M / (T_M*p_n) in kg/m³				Gasdichte (r) in kg / m³			1,2	1,21
V_M = V_n * r_n / r_M in m³/s				Volumenstrom (V) in m³/Sekunde			0,3	0,297
w_M = V_M / (d² * p/4) in m/s				Gasgeschwindigkeit (w) in m/s			21	20,8
Formel nur bei Temperaturgleichheit: u_M = u_n * p_n / p_M in m²/s				kinematische Viskosität (u) in m²/s (mm²/s * 10^-6 = m²/s)			15,15 *10^-6	15,00 *10^-6
p_{dyM =} r_M * w_M² / 2 in Pa				mittlerer dynamischer Druck der Teilstrecke (p_dyM) in Pa				261
Einzelwiderstände:				(Bezeichnung für nachfolgend, vorher, Anfang bzw. Ende bei den Teilstrecken immer in Flussrichtung gesehen.)
Bezeichnung	Stck	z	Stck*z
Ausblasstutzen	1	1	1	Druck (p_n) entsprechend dem für den Normalzustand des Gases definierten Wert in Pa				101 300
				Geschätzter Druck am Beginn der Teilstrecke in Pa. Bei großen Abweichungen, von dem sich später in Zeile 11 ergebenem Wert, ist die Rech- nung mit dem neuen Wert zu wiederholen. Wenn Nebenstrang: Wert aus Zeile 11 übernehmen				[1] 104 500

				Mittlerer statischer Druck (p_M) in der TS in Pa (Zeile 1 + Zeile 8) / 2 - p_dyM				[2] 102 313

Einzelwiderstände: Summe ( Stck*z )			1	Þ * p_dyM= 261	261 Pa		[3] Druckverlust durch Einzelwiderstände
Nach Formeln 10.1 Überwiegend im Übergangsbereich nach 10.2: Dp = { 0,25 / [ ( log₁₀ (15 * u_M / (w_M * d) + k / (3,715 * d) ))² ] } * l * r_M * w_M² / (d * 2) in Pa					4 129 Pa		[4] Druckverlust durch Rohrreibung
p_hydro = Dh * r_M * 9,81 m/s² Vorzeichen beachten (negativer Wert von Dh ergibt Druckgewinn)					0 Pa		[5] Druckverlust durch hydrostatischen Druck
Nach Herstellerangaben					0 Pa		[6] Druckverlust durch Geräte
Summe der Zeilen 3 bis 6					4 390 Pa		[7] Druckverlust der Teilstrecke

Entsprechend dem Anfangsdruck der nachfolgen TS, bzw. am Ende der Leitungen Atmosphärendruck im Bereich des Ausblasstutzens in Pa (1,013 bar = 101 300 Pa)					100 125 Pa		[8] Druck am Ende der Teilstrecke
Zeile 8 plus Zeile 7 Nur für verzweigenden Leitungen: Wenn dieser Druck niedriger ist als der Druck an der Stelle, wo diese TS von dem anderen Strang abzweigt, ist diese TS ein Nebenstrang und zu drosseln. Wenn dieser Druck höher ist als der Druck im Strang, wo er abzweigt, gehört diese TS zum Hauptstrang, und der andere Strang ist entsprechend zu drosseln.					104 515 Pa		[9] Druck am Anfang der Teilstrecke (ohne Drosselung)
Zeile 11 minus Zeile 9 Wenn Nebenstrang: Drosselung zur Erhöhung des Anfangsdrucks der Teilstrecke.					0 Pa		[10] zusätzlicher Drosselverlust
Wenn Hauptstrang : Wert aus Zeile 9 übernehmen. Wenn Nebenstrang: Druck des Hauptstranges im Bereich der Abzweigung hier übernehmen. Der Wert ist gleichzeitig der Enddruck für die vorhergehende TS					104 515 Pa		[11] Druck am Anfang der Teilstrecke (Um die Druckverluste höher als der Enddruck)

Da die Fördergasdichte ungefähr der Dichte der Umgebungs-Atmosphäre entspricht, wird der Druckverlust durch den Höhenunterschied der Teilstrecke 2 (Zeile 5) von 1112 Pa kompensiert durch den höheren Atmosphärendruck im Ansaugstutzen der Teilstrecke.

Der Druckverlust der gesamten Anlage (D_pgeA) beträgt:
	Anfangsdruck der Teilstrecke 4 von	104 515 Pa
minus	Enddruck in der Teilstrecke 3 von	87 044 Pa
	Druckdifferenz (D_pgeA) =	17 471 Pa

Für die Auswahl des Ventilators sind die Angaben nach 10.10 zu berücksichtigen.
Im Ventilatoransaugstutzen herrscht ein Druck von 87 044 Pa. (Enddruck der Teilstrecke 3)

Bei einem Volumenstrom von 0,3 m³/s bezogen auf den "Norm"-Gaszustand wäre der Volumenstrom
bezogen auf den Druck im Ansaugstutzen nach Formel 10.4
V_n = p_n * V_n / p_n = 101 300 Pa * 0,3 m³/s / 87 044 Pa = 0,349 m³/s

Die Gasdichte im Ansaugstutzen beträgt nach Formel 10.5
r_x = r_n * p_x / p_n = 1,2 kg/m³ * 87044 Pa / 101 300 Pa = 1,031 kg/m³

Der benötigte Ventilator muss einen Volumenstrom von 0,349 m³/s, mit einer Dichte von 1,031 kg/m³, fördern und dabei eine Druckerhöhung von 17 471 Pa erbringen.
Der Leistungsbedarf des Ventilators an seiner Antriebswelle beträgt:
	gewählt: Sicherheit (s) = 15%, Wirkungsgrad (h) geschätzt = 70%

Damit aus den Datenblättern der Lüfterhersteller, die auf eine Gasdichte von 1,2 kg/m³ im Ansaugstutzen bezogen sind, ein Ventilator ausgewählt werden kann muss zuerst die Druckerhöhung ermittelt werden, die der Ventilator bei dieser Gasdichte erzeugen müsste.
Nach umgestellter Formel 10.12: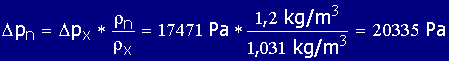

Aus den Herstellerunterlagen kann jetzt ein Ventilator bestimmt werden, der bei einem Volumenstrom von 0,349 m³/s eine Druckerhöhung von 20,335 kPa erbringt. Der dort angegebene Leistungsbedarf von angenommen 11659 Watt ist auf die Förderung von Gas mit einer Dichte von 1,2 kg/m³ bezogen und muss auf eine Dichte von 1,031 kg/m³ umgerechnet werden.
Nach Formel 10.13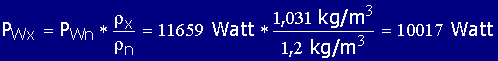

10.10 Ventilatorbestimmung unter Berücksichtigung der Gasdichte.

Wenn die saugseitigen Widerstände einen Druckverlust von über 5 000 Pa verursachen, sollten die dadurch entstehenden Dichte- und Volumenänderungen, der Luft im Ansaugstutzen des Ventilators, berücksichtigt werden.

Die Angaben der Ventilatorhersteller bezüglich Volumenstrom (V), Druckerhöhung (Dpt) und Leistungsbedarf (P) gehen außer in besonders angegebenen Fällen davon aus, dass im Ventilatoransaugstutzen Gas mit einer Dichte von
1,2 kg/m³ vorhanden ist.
Dies ist der Fall, wenn Luft mit einer Temperatur von 20° C bei einem Luftdruck von 1,013 bar ohne nennenswerte Widerstände durch Rohrleitungen zum Ansaugstutzen des Ventilators gelangt.

In anderen Fällen ändert sich unter Beibehaltung des Volumenstroms die Druckerhöhung (Dpt) und der Leistungsbedarf des Ventilators im Verhältnis r_x zu r_n.

Dp_tn	Differenzdruck des Ventilators im Normalfall bei einer Gasdichte von 1,2 kg/m³ im Ansaugstutzen
Dp_tx	Differenzdruck des Ventilators bei der Gasdichte x
r_n	Gasdichte im Normalfall 1,2 kg/m³
r_x	Dichte des Fördergases im Zustand x
P_wn	Leistungsbedarf im Normalfall
P_wx	Leistungsbedarf bei der Gasdichte im Zustand x

Beispiele:

Um die Beispiele übersichtlicher zu halten, wird der Wirkungsgrad des Ventilators nicht erwähnt - hierfür siehe 2.5, außerdem ist der Volumenstrom (V) in m³ pro Sekunde angegeben und nicht auf m³ pro Stunde umgerechnet.

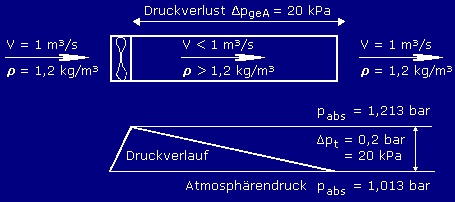
Fall 1
Widerstände druckseitig.

Da im Ventilatoransaugstutzen Luft mit einer Dichte von 1,2 kg/m³ vorhanden ist (Normalfall), kann der Ventilator aus den Kennlinienangaben der Hersteller ausgewählt werden.

Er muss bei einem Volumenstrom von 1m³/s eine Druckerhöhung (Dpt) von
20 kPa erbringen.

Bei der Druckverlustberechnung der Rohrleitung sollte berücksichtigt sein,
dass hier ein Gas gefördert wird,
das durch den Ventilatordruck eine größere Dichte aufweist
und dadurch auch geringere Luftgeschwindigkeiten in den Rohren auftreten.

Leistungsbedarf: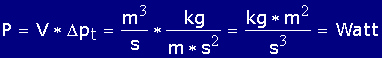
f10_14.gif (912 Byte)

P = 1 m³/s * 20 kPa = 20 kW

Würde statt Luft mit der Dichte 1,2 kg/m³ ein ebensogrosser Volumenstrom, z.B. Abgase,
aber nur mit einer Dichte von 1,0 kg/m³ in den Lüfter eintreten, so wäre bei einer gewünschten Druckerhöhung
von 20 kPa der Energiebedarf auch: P = V * Dp_t = 1 m³/s * 20 kPa = 20 kW

Um hierfür dann aus den Kennlinien, die auf eine Dichte von 1,2 kg/m³ bezogen sind,
einen Ventilator auswählen zu können, muss die erforderliche Druckdifferenz von 20 kPa
bei einer Dichte von 1 kg/m³ umgerechnet werden auf einen Wert, den der erforderliche Ventilator
bei einer Dichte von 1,2 kg/m³ erzeugen müsste.
Nach Formel 10.12: Dp_tn = Dp_tx * r_n / r_x = 20 kPa * 1,2 kg/m³ / 1kg/m³ = 24 kPa

Aus den Kennlinien kann nun ein Lüfter bestimmt werden, der bei einem Volumenstrom von 1 m³/s
einen Differenzdruck (Dp_t) von 24 kPa erzeugt.
Der dort angegebene Leistungsbedarf (P = Dp_t * V = 24 kPa * 1 m³/s = 24 kW)
ist auf eine Dichte von 1,2 kg/m³ bezogen und muss nach 10.12 umgerechnet werden
auf die vorhandene Dichte von 1 kg/m³: P_x = P_n * rx / r_n = 24 kW * 1 kg/m³ / 1,2 kg/m³ = 20 kW

Sollte es sich hierbei um warme Luft mit der Dichte 1 kg/m³ handeln, ist zu beachten, dass bei Betriebsbeginn, solange noch kalte Luft mit einer Dichte von 1,2 kg/m³ gefördert wird, ein Leistungsbedarf von 24 kW besteht.

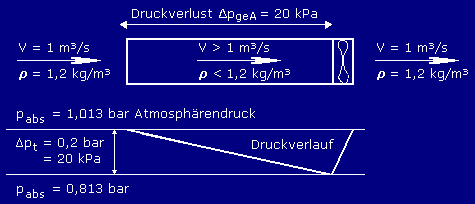
Fall 2
Widerstände saugseitig

Durch den vom Ventilator erzeugten Unterdruck nimmt die anfängliche Dichte der Luft immer mehr ab, wobei der Volumenstrom und damit auch die Luftgeschwindigkeit ansteigen.
Am Saugstutzen des Lüfters herrscht ein Absolutdruck*
von 0,813 bar.
Die Luftdichte beträgt dort nach Formel 10.6:

r_x = p_absx / ( 0,00287 * T_x) r_x = 0,813 / ( 0,00287 * 293 ) = 0,97 kg/m³

Da sich der Massenstrom im Leitungsverlauf nicht ändert (V_n * r_n = V_x * r_x)
beträgt der Volumenstrom im Ventilatoransaugstutzen:
V_x = V_n * r_n / r_x Vx = 1 * 1,2 / 0,97 = 1,24 m³/s

Es wird also ein Lüfter benötigt, der bei einer Gasdichte von 0,97 kg/m³ einen Volumenstrom von 1,24 m³/s fördert
und dabei eine Druckerhöhung (Dp_t) von 20 kPa erzeugt.
Er benötigt dafür eine Leistung von P_x = Dp_t * V_x = 20 kPa * 1,24 m³/s = 24,8 kW

Für die Auswahl des Lüfters nach Kennlinien, die auf eine Dichte von 1,2 kg/m³ im Ansaugstutzen bezogen sind,
ist nun die Druckdifferenz zu ermitteln, die dieser Ventilator bei einer Dichte von 1,2 kg/m³ erbringen müßte.
Nach Formel 10.12: Dp_tn = Dp_tx * r_n / r_x = 20 * 1,2 / 0,97 = 24,74 kPa

Anhand der Kennlinien ist nunmehr bei einem Volumenstrom von 1,24 m³/s ein Ventilator mit einer Druckdifferenz von 24,74 kPa zu suchen.
Der dort angegebene Leistungsbedarf: (P_n = V * Dp_tn = 1,24 * 24,74 = 30,7 kW) wird nur benötigt, wenn das Fördergas eine Dichte von 1,2 kg/m³ hätte.
Bei einer Dichte von 0,97 kg/m³ ist er nach 10.13: P_x = P_n * r_x / r_n = 30,7 * 0,97 / 1,2 = 24,8 kW

Fall 3 Widerstände saug- und druckseitig.

b_fall3.gif (3766 Byte)

Da für die Ermittlung des Ventilators Volumenstrom und Dichte des Gases in seinem Ansaugstutzen bekannt sein müssen (die Druckerhöhung (Dp_t) mit 20 kPa wurde bereits vorgegeben), kann zuerst die Dichte ermittelt werden.
Nach Formel 10.6 ist sie bei einer Temperatur von 20° C:
r_x = p_absx / ( 0,00287 * T_x ) = 0,913 / ( 0,00287 * 293 ) = 1,086 kg/m³

Der Volumenstrom im Saugstutzen ist da der Massestrom (V_n * r_n = V_x * r_x) sich nicht ändert
V_x = V_n * r_n / r_x = 1 * 1,2 / 1,086 = 1,1 m³/s

Diese Werte sollten nicht neu sein da sie bereits zur Ermittlung der Druckverluste für die Leitung erforderlich waren.
Der Energiebedarf des Ventilators ist bei dem Volumenstrom von 1,1 m³/s
und der Druckerhöhung (Dp_t) von 20 kPa:
P_x = V * Dp_tx = 1,1 m³/s * 20 kPa = 22 kW

Damit ein Ventilator nach den Angaben der Hersteller, die auf einer Gasdichte von 1,2 kg/m³ im Ansaugstutzen basieren, bestimmt werden kann ist die Druckerhöhung zu ermitteln die er bei dieser Dichte erzeugen müßte.
Nach Formel 10.12: Dp_tn = Dp_tx * r_n / r_x = 20 * 1,2 * 1,086 = 22,1 kPa

In den Herstellerlisten ist ein Ventilator zu suchen, der bei einem Volumenstrom von 1,1 m³/s
eine Druckerhöhung (Dp_t) von 22,1 kPa erzeugt.
Der darin vermerkte Leistungsbedarf von (P_n = V * Dp_t = 1,1 * 22,1 = 24,3 kW)
ist auf die Dichte von 1,2 kg/m³ bezogen und entsprechend Formel 10.13 zu korrigieren:
P_x = P_n * r_x / r_n = 24,3 * 1,086 / 1,2 = 22 kW

10.11 Einschränkungen

Die Annahme, dass eine Anlage im Hochland der Anden, wo die Luft sehr dünn ist, besonders preiswert arbeitet, da nicht so viel Energie benötigt wird um einen Kubikmeter der leichteren Luft zu bewegen, ist nur teilweise richtig, da in vielen Fällen die abzusaugenden Luftmengen vergrößert werden müssen, z.B. um Staubaustritt zu vermeiden oder die Luftgeschwindigkeit in den Rohrleitungen erhöht werden muss, damit die abzusaugenden Stoffe in Schwebe bleiben. Wenn Sie jedoch, wie in dem Berechnungsbeispiel, die abzusaugende Luftmenge auf normalen Luftdruck (1013 mbar) beziehen, erhalten Sie höhere Druckverluste und höheren Energiebedarf.